直角の定義。それはこの世のすべて
少し前にキーボードを変えた。いままで使っていたIBM製のキーボードは、キータッチといい耐久性といい、かなりお気に入りだったのだけど、もう7,8年使っているので、さすがにヘタって来た。「A」のキーや、エンターキーの刻印なんて、かすれちゃって、ほとんど見えないくらいだ。ブラインドタッチができるわけじゃないけど、まあ、一部のキーの刻印が見えなくなるくらいなら、使用に問題はない。
でも、そろそろ替え時かなあ……と、しばらく前から思いはじめた。ある日突然、「A」キーが反応しなくなるなんて事態はごめんだ。とろこが、いざ変えようと思っても、なかなか好みのタイプが見つからないんだよね。前にも書いたことがあるから、覚えておいでの方もいるだろうけど、ぼくは英語キーボードじゃないとイヤなんだよ。ダメとは言わない。イヤなんだ。要するに、ワガママに近いってことだね。ノートパソコンは日本語キーボードでも使えてるんだから。
ま、イヤなものはしかたない。英語キーボードで、いいものがないか探してみたら、よさげなのを見つけたので買ってみた。たぶん、パソコンに詳しい人なら、「FILCO」というブランドを、ご存じだろうと思う。ダイヤテックという、日本の小さな会社が作ったブランドだ。ダイヤテックは、FILCOブランドで、さまざまなキーボードを発売している。
で、ぼくが買ったブツは、こういうヤツ。
英語キーボードなのは必須条件だけど、無線式(Bluetooth)は、とくに必須ではなかった。でも無線は大好きなので、むしろうれしい。高くなるけどね(苦笑)。ちなみに購入価格を聞いたら、ビックリするかも。13,000円ぐらいするんだぜ。回転しない寿司屋に行けちゃうよ(苦笑)。
もっとも、このキーボードの特徴は、無線式という部分ではなくて、メカニカルスイッチを採用していることなんだ。メカニカルスイッチは、キーを一番下まで押しきる必要がないから、長時間の入力作業に向いていると言われる。つまり疲れにくいわけだ。
使ってみると、たしかに軽快なタッチで、パチパチ入力できる。悪くない。でもIBMのキーボードとは、やっぱりタッチが違うから、慣れるまで少し時間がかかりそうだね。だいぶ慣れたけど、まだ少し違和感がある。一時間以上使っていると、指先がビリビリするんだ。どうやら、キーを強く叩きすぎているらしい。だから、指先が疲れてくると、執筆をノートパソコンに切り替えて、あの平べったくて、ペシャペシャしたキーボードで打っている。すると、ノートパソコンのキーボードも、これはこれで悪くないかも……なんて思ったりして(笑)。
さて、小ネタというか脱線はこのくらいにして、そろそろ本題。今回は久しぶりに科学エッセイだよ。お待ちかねの人も、そうでない人も、ぜひ読んでいただきたい。損はさせませんぜ(笑)。
2008年の5月9日に、うちの感想掲示板に「フェルマーの最終定理の変形」と題する投稿があった。いかにもScript1にふさわしい感じのタイトルじゃないか。
と思ったら……
残念ながら内容の方は、有意義に感じられるものではなかった。「こんにちは」でも「こんばんは」でもなく、少々、人を小バカにしたようなシロモノだ。もしかしたら、いまの若い方は、それでいいのかも知れないが……ぼくのような青春中期に差し掛かると、少し、ほんの少しだけ、礼儀という名の常識に対して、若い方よりも敏感のようだ。だから、あまりにも唐突で、かつ内容が不明瞭だと、掲示板荒らしではないかと疑ってしまう(事実そう疑って、投稿者がリンクしたメルアドは削除した)。
ところが、一週間経ったいまも、その投稿が、感想掲示板のトップにあって、それを見るにつけ、ぼくの心は痛む。これは本当に掲示板荒らしなのか? それとも、ぼくの誤解で、対応が間違っていただろうか? だとしたら、この投稿者は、密かに傷ついているかもしれない……
ひるがえって考えると、そもそも、最近雑文ばかりで(それも途切れがちだ)、まともなエッセイを書いていないから悪いんじゃないのか? 幸い、ゲームシナリオも一段落ついたところだから(まだ終わってはいないんだけど)、本腰を入れてエッセイを書く時間はある。
というわけで書きます。
フェルマーの名が出たから言うわけじゃないけど、じつは前から、数学を主題にしたエッセイを書いてみたいと思っていたんだ。いろいろ書いたエッセイの中で、何度か数学の話題には触れているけど、数学そのものを主題にしたエッセイを書いたことはないからね。
ただ……数学のエッセイを書くのは、大きな問題がある。ぼくには数学の才能がほとんどないんだ。だから、数学を主題にしたエッセイは避けてきたというのもある。それでもいま、コンピュータの前に座って、しかも新しいキーボードを前にして、自分がなにを書きたいかを自問すると、それは「数学」なんだ。例の投稿に、ちょいと負けん気を刺激されているだけかも知れないが(苦笑)。
まあ、動機はなんでもいい。とにかく、がんばってみよう。みんなも準備はよろしいかな? ぼくと一緒に、数学の旅に出発しよう。
そもそも「数」とはなんだ?
いきなり哲学的な問題だな。でも、ここを通らずに数学のエッセイをはじめるわけにはいかないから、ぼくのいつもの癖で、歴史の中に答えを求めてみよう。
そもそも数とは、物の「個数」を数えるために誕生した。われわれが「数」を必要としたのは、ビジネスをしたかったからだ。ビジネスなんて言葉を使うと、いかにも現代的だけど、ぼくらは文明を築くずっと前から、物々交換という商取引を行ってきた。肉と魚、あるいは野菜と果物などなど、交換できるものなら、なんでも取引されただろう。
物々交換がはじまった最初のころは、本当に素朴な取引しか行われなかっただろうね。手に持てるだけの魚と、やはり手に持てるだけの肉とか、馬の背に乗せられるだけの果物と、やはり馬の背に乗せられるだけの穀物とか……まあ、そんな具合だったろう。
でも、そんな目分量では、すぐに行き詰まる。手の大きな人と小さな人では不公平だし、そもそも、たくさんの物を交換できない。たとえば、小麦3袋と、米3袋を交換するぐらいだったら、数はいらない。目で見て同じだけあるとわかるから。でも、小麦が100袋、米が100袋あったらどうする? あるいは、1000袋あったら? いやいや、10000袋かもしれない。
こうなるともう、人類はイヤでも物の数を数えないわけにはいかない。こうして、もっとも原始的な「数」という概念が生まれた。
概念というのは、一度思いつくと、様々に応用が利く。個数を数えるだけでなく、すぐに「重さ」を表すことにも使えると気づいただろうし、それどころか「広さ」にも使えると気づいたはずだ。広さを「数」で表すことができれば、不動産取引がやりやすくなったことだろう。
中でも古代エジプトは、ナイル川の氾濫で、毎年、豊饒な土地を手に入れる代わり、土地と土地の境界線が不明瞭になるというリスクも負わなければならなかった。たぶん、農民同士のトラブルは絶えなかったはずだ。
そこで「数」を使って広さを「表す」だけでは不十分で、広さを「計る」必要が生じた。こうして生まれたのが幾何学だ。幾何学は学問の中で、もっとも歴史が長いものの一つだろう。ちなみに、幾何学を表す英語「geometry」は、もともと「土地を測る」という意味の言葉だった。
いまぼくは、幾何学を学問と呼んだけれど、古代エジプト人の用いた幾何学は、あくまでも土地の測量や、天体の運動を計る道具であって、学問と呼ぶにはまだ早かった。とくに数学の一分野として扱われるようになるには、まだまだ時間が必要だ。
数という概念が、本格的に研究される対象になったのは、古代ギリシア時代だ。歴史に登場する最初の数学者(哲学者と言った方が、より正確だけど)は、ギリシア七賢人の一人、ミレトスのタレスのはずだ。紀元前624年に生まれたとされている。タレスは、世界ではじめて、ピラミッドの高さを測った人物だ。その方法は、気がついてみればじつに簡単。まず、地面に落ちた影と自分の身長を比較しておいて、それから同じ時のピラミッドの影の長さを測る。すると、先ほど比較しておいた、自分の影と身長の比率が適応できるので、ピラミッドの高さがわかる。
すばらしい!
だが、これはまだ「道具」の段階だ。いやいや、数学を道具に使うのは大いにけっこうなことだが、経験や観測によって得られたデータを、計算するための学問を、純粋に「数学」と呼ぶことはできない。
たとえば、タレスは「半円の弧に対する円周角は90度になる」ことを発見して、それは「タレースの定理」と呼ばれている。じつに立派な発見だ。でも、たぶんタレースの定理は、タレスが発見した物ではない。彼よりずっとずっと昔の大工(建築家)か、あるいは天文学者が、発見したに違いない。タレスは、経験的に知られていた現象を、言葉として定義しただけだろう。誤解を恐れずに言うなら、そんなこと、小学生にもできる。数学者の仕事ではない。
では、どうすれば、数は数学になれるのか?
それは、数が自然現象や経験を離れ、便利な道具から、なんの役にも立たないガラクタになったときだ。そのときこそ、数学の誕生と言える。
その意味で、最初の数学者は、ピュタゴラスだと、ぼくは思う。
ピュタゴラスは、紀元前582年にエーゲ海東部の島サモスで生まれた。それからの彼の人生は謎に包まれているのだけど、伝説によれば、二十年近く旅を続けて、エジプト人やバビロニア人から、さまざまな算術のテクニックを学んだそうだ。そして、故郷のサモスに戻って学問所を開いたけれど、政治的な理由もあってうまくいかず、古代ギリシアが植民地にしていた、イタリアのクロトンに渡って、そこでピュタゴラス教団を作った。古代ギリシアには、哲学者の名に、生まれた場所や、活動した場所を付ける風習があるので、ピュタゴラスも「サモスの賢人」とか、「クロトンの哲学者」と呼ばれている。
さて、それはそうと、なぜ彼のことを、最初の数学者だと思うかだけど、なんとピュタゴラスは、「数には数の論理がある」という思想を説いたんだ。ピュタゴラスによって、数は物を数える道具から、数それ自体に「価値」が見いだされたんだよ。
たとえば、ピュタゴラスが注目した数の中で、とくにお気に入りだったのは「完全数」だ。完全数とは、その数自身を除く約数の和が、その数自身と等しい自然数のことだ。
わーぉ。そんなこと言われても、サッパリわからないわ。と言う声が、どこかから聞こえる。そもそも約数ってなにさ? という声が。わかってるって。解説しますよ。子供でもわかるように(笑)。
約数とは、その数を割って、余りのでない数のことだよ。それでは6の約数を探してみよう。6を2で割ると答えは3で、余りは出ないね。だから2は、6の約数だ。逆に3で割ったら答えは2だから、もちろん余りは出ない。オーケー、3も6の約数に加えよう。
これで全部かな?
おっと、忘れるところだった。1でも割れるじゃないか。その場合の答えは6だ。これまた逆に、6で割っても答えは1だから、余りは出ないね。でも待って。6は約数を探していた、その数自身だから、これは含めないことにしよう。
と言うわけで、6の約数は、1,2,3の三つあることがわかったかな?
さーて、お立ち会い。ここで、暗算でできる、簡単な計算をやってみて欲しい。いま上に挙げた、1、2、3を足してみてくれないかな。式にすると「1+2+3」。さあ答えは?
6だよね。
これが完全数なんだ。約数の和が、その数自身になる数のことなんだよ。いま簡単に6を見つけたけど、完全数を探すのは、じつは、すごく難しい。6のつぎに出てくる完全数は28。そのつぎは496、さらに4番目になると、なんと8,128だ。この辺でやめとこう……え?、なに? 5番目も教えろだって? いいよ、33,550,336だ。ついでに6番目も書いとこう。8,589,869,056さ。
これでホントに終わり。だって、ウィキペディアの記事に、ここまでしか載ってないので、コピペできないから(笑)。
ともかく、俗っぽい言い方だけど、完全数は先へ行くほど、巨大な桁数になって行く。とてもじゃないけど、人間が紙とペンを使って計算できるモノじゃない。ピュタゴラスの時代は、おそらく4番目の8,128までしか知られていなかったはずだ。
現在はもちろん、コンピュータが人間に代わりに計算して、完全数を探している。ウィキペディアによると、2006年の時点で、44番目まで見つかっているようだ。その大きさたるや、もはや想像を絶する。
さて。完全数については理解できたかな?
では、話をピュタゴラスに戻そう。彼は、この数をもっと見つけたいと願っただろうけど、それで満足したわけではない。ピュタゴラスの本当の願いは、もっと深い意味を見いだすことだった。そのために、どれほどの時間を研究に費やしたのか歴史は教えてくれないけど、ピュタゴラスがいくつかの発見をしたことはわかっている。
たとえばピュタゴラスは、完全数は約数の和に等しいだけでなく、つねに自然数の連続した和として表せることを発見した。書き出すのが面倒だから、ここでは、6と28だけお見せしよう。
| 6 |
= |
1+2+3 |
| 28 |
= |
1+2+3+4+5+6+7 |
ほらね。自然数の連続した和になってるだろ。わざわざ書き出さないけど、496も、8,128も、ちゃんとこの法則に従っている。お疑いなら、496は、1から31までを、8,128は、1から127までを足し算してくれればわかるはずだ。
あるいは、完全数と『2のべき』との深い関係も、ピュタゴラスは発見していた。
わーぉ。また難しい言葉。2のべきってなにさ? という声が、PCモニターの向こう側から聞こえる気がする。うーむ、幻聴が聞こえるようになっちゃおしまいだな。え、なに? 幻聴じゃないから、説明をしろって? はいはい、わかりました。例によって子供にもわかるように説明しますよ。
べつに難しいことはなにもないんだ。べきとは、要するに「かけ算の反復」のことだ。だから『2のべき』とは、2×2×2×2……ということ。教科書に「2n」なんて書いてあったのを覚えてるだろ。普通は、いまのように2のn乗という形で書くけど、このエッセイは算術を解説するわけじゃないから、まあ、細かいことは忘れてくれてもいい。
ともかく、2と2のかけ算で、一番簡単なのは、2×2だね。これの答えは4だ。だから4のことは「2のべき数」と言うことができる。もう少し計算してみよう。まず2のべきをいくつか書き出すよ。
| 2×2 |
= |
4 |
| 2×2×2 |
= |
8 |
| 2×2×2×2 |
= |
16 |
| 2×2×2×2×2 |
= |
32 |
この結果から、4、8、16、32は、2のべき数だとわかったね。ではつぎに、これら2のべき数の、約数を書き出してみよう。
| 4 |
、 |
1,2 |
| 8 |
、 |
1,2,4 |
| 16 |
、 |
1,2,4,8 |
| 32 |
、 |
1,2,4,8,16 |
ここまではオーケー? まだ寝ないでついてきて! つぎに、この約数を足してみよう。
| 4 |
、 |
1+2 |
= |
3 |
| 8 |
、 |
1+2+4 |
= |
7 |
| 16 |
、 |
1+2+4+8 |
= |
15 |
| 32 |
、 |
1+2+4+8+16 |
= |
31 |
さあ、みんなは、このミステリーに気づいたかな? わかりやすいように、上の表の注目すべきところを赤くしておいたよ。さあ、よく見てくれ。また、見ることが困難な人は、ぜひ想像してみて欲しい。約数の元になった数字と、それを足した結果を……ほら、わかったね。
そうなんだ。2のべき数の約数を足すと、驚くべきことに、元の数から、いつも1足りないんだよ! これは2のべき数が、つねに「完全性を微妙に欠いている」と考えていいんじゃないか?
ところが、このミステリーのクライマックスはこれからだ。いま見てきたように、約数の和が、その数自身より1だけ小さい数を、いくらでも見つけられるのに、どういうわけか、1だけ大きい数はなさそうなんだ。少なくとも古代ギリシア人は、そんな数を一つも見つけられなかった。そして、ここが重要なんだけど、そんな数がこの世に存在しないことを「証明」することもできなかったんだ。
このエッセイを辛抱強く読んでくれている読者のために、もう一つ秘密を教えよう。じつは、現代の数学者も、1だけ大きい数を発見できていないし、それが存在しないことを証明することもできない。ピュタゴラスに解けなかった謎を、ぼくらもまだ解けていないんだ。
どうかな。そろそろ数学というモノが、どんなものかわかってきた?
もしも、現代の数学者のだれかが、いま上に挙げた、1だけ大きい数字がこの世に存在しないことを証明したとしよう。2500年に渡るミステリーが解けたら、それはすごいことだよね。
と同時に、たぶん、ほとんどの人がこう思うだろう。それってなんの役に立つの? と。その質問には簡単に答えられる。なんの役にも立たないとね。だからこそ、ぼくは大きな声で宣言しよう。
それが数学だ!
われながら、すごく誤解されそうな解説だなあ(苦笑)。高潔なる数学のことを、まるで子供のオモチャみたいに言ってる。でも、気持ちは汲んでもらえるよね?
よく「基礎研究」はお金にならないと言われる。企業は、手っ取り早く、売れる商品を作りたいから、地味な基礎研究に研究費を出すのを渋るわけさ。数学には、ちょっとそんな所があるかも知れない。とくに、いままで説明したような「数」そのものを扱う数学は、数学の中でも、さらに基礎的な部分だから、応用できる分野があまりないように思える。こういった「数」そのものを扱う分野は、現在では「数論」と呼ばれていて、近代数論を作り上げたのは、18から19世紀に活躍したのドイツの数学者、ヨハン・カール・フリードリヒ・ガウスだ。近代数学のほとんどの分野に影響を与えたと言われる、大数学者だ。その彼が、有名な言葉を残している。
数学は科学の女王であり、数論は数学の女王である。
なんというエレガントな言葉。日本語でさえ、その響きに聞き惚れそうだ。なんの役にも立たなく見える数学は、じつは科学の女王なんだよ。彼女がいなければ、科学という国は栄えない。比喩的ではなく、もうちょい具体的に言うと、数学が「新しい概念」を生み出してくれなければ、新しい科学は発展しないんだ。なぜなら、その科学を表す言葉が数学なのだから。一例を挙げるなら、ニュートンが万有引力の法則を考えられたのは、微積分という方法を考えついたからにほかならない。このように数学は、科学の母であり、まさに女王なんだ。
だから、まだ科学の女王の話を続けよう。
このエッセイを書くキッカケは、フェルマーの最終定理の名がついた掲示板の投稿だと書いた。そしてぼくは、ピュタゴラスの話をしたのだから、ここで「ピュタゴラスの定理」に触れないわけにはいかないだろう。
なんで?
と思ったあなた。なぜなら、かの有名な、フェルマーの最終定理は、ピュタゴラスの定理が、その基礎になっているからなんだ。
17世紀、フランスの数学者、ピエール・ド・フェルマーが残した問題の中で、この問題(予想)だけが最後まで残った。数多くの数学者が、その神秘のベールをはがそうと挑戦しては挫折していった。そして360年が経ち……とうとうイギリスの数学者、アンドリュー・ワイルズが、ベールの中に隠れた彼女のほほ笑みを見ることができたのだ。
この、多くのドラマに彩られた、フェルマーの最終定理(現在ではフェルマー・ワイルズの定理と呼ぶのが正しい)の、基礎を作り上げたのがピュタゴラスなのだから、彼の話を続けよう。
まずはピュタゴラスの定理を、言葉で表現してみよう。
直角三角形の斜辺の二乗は、他の二辺の二乗の和に等しい。
また、サッパリわかりませんという声が、PCモニターの向こう側から聞こえる(苦笑)。念のために申し上げておくと、たぶん中学の教科書に出てきて、義務教育を受けるすべての子供たちが、一人残らず覚えなければならない定理なんだけど……はいはい、わかったよ。そんなの覚えた記憶さえないって言うんだろ(笑)。
べつに難しいことは、なにもないんだ。頭の中で直角三角形を思い浮かべるのが難しい人のために、図を書いてみよう。
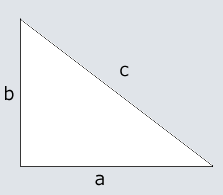
わかるよね。この図で、直角三角形の斜辺(斜めになっている辺)を、cと呼ぶことにしよう。そして、水平な辺をa、垂直な辺をbとする。
これで、先ほどの言葉で表現した定理を、数式に置き換える準備ができた。よろしいかな。言葉を分解して、わかりやすくしてみるよ。
直角三角形の「斜辺」の「二乗」は、「他の二辺」の「二乗」の「和」に「等しい」
ほら、もう、あなたにも式が作れるよね。
a2+b2=c2 (aの二乗+bの二乗=cの二乗)
ね、たったこれだけのことさ。なのに、驚くべきことは、この簡単な式は、どうやら、すべての直角三角形に当てはまるようなんだ。待ってくれ。直角三角形は、無限に作り出せる。辺の長さを変えるだけでいいのだからね。なのに、そのすべての直角三角形に、上の式が成り立つことを調べるには、どうしたらいいんだろう?
一番簡単な調べ方は、すべての直角三角形について「計算」してみることだ。これなら小学生にもできるだろう。ただし、その小学生が、老人になるまで計算しても、その長い旅は終わらない。それどころか、宇宙の寿命が(寿命があればだが)尽きるまで計算し続けても、終わることはない。なぜなら、計算すべき直角三角形は、無限にあるのだから。
ここで、またみんなに、秘密を教えよう。じつは、ピュタゴラスの定理は、ピュタゴラスが発見したわけじゃないんだ。彼に先立つこと、千年以上も前から、中国やエジプトで知られていた。ただ彼らは、そのつど、必要な計算にこの定理を用いただけで、すべての直角三角形に当てはまることを調べようとはしなかった。建物を造るときに、正しい答えが得られれば、それでよかったんだ。
ところがピュタゴラスは違った。この定理が、すべての直角三角形に成り立つことを「証明」したんだよ。だからこそ、この定理に、彼の名が永遠に刻まれた。
さあ新しい言葉だぞ、諸君。「証明」。それは数学にとって、もっとも重要な考え方だ。さっきぼくは、ピュタゴラスの定理を調べるには「計算」すればいいと書いた。ただしそれは、永遠に終わらない計算だ。永遠に終わらないのなら、それは調べたことにはならない。だが、もしも、計算に頼ることなく、すべての人を納得させる「説明」ができたらどうだろう?
そう。証明とは、だれもを納得させる「説明」だ。ここで重要なのは、「だれもを納得させる」という部分だ。この世のほとんどの問題には、賛成する者と反対する者が存在する。たとえば、政治家が税金を安くすると宣言したとしよう。国民はみんな賛成するように思えるけど、実際は反対する者だってたくさんいる。税金を安くして保証を削られては困るからだ。このように、人間社会の問題に、白黒付けるのは容易ではない。
ところが数学の世界は違う。白か黒しかない。曖昧さも、利権も、感情的軋轢も許されない。数学に許されるのは「理(ことわり)」だけなんだ。だからこそ、数学の「証明」は、「すべての人」を「完全」に「納得」させることができる。科学の中で、そんなことができるのは数学だけだ。
さて。この「証明」という方法は、ピュタゴラスに先んじて、すでにタレスが、その片鱗を示している。いま再び、ピラミッドの高さを計算したタレスのことを思い出して欲しい。
彼は、自分の影と身長を測って比較し、それからピラミッドの影を計って、ピラミッドそのものの高さを求めた。このとき、彼はこう考えたのだ。
同じ時間の、同じ場所は、太陽の光が等しく当たっているのだから、影と実体の比率は、その実体が小さくても(人間)、どれほど大きくても(ピラミッド)、まったく同じはずだ。よって、小さい物の影と実体の比率を求めれば、大きな物の影の長さから、その実体の高さを計算できる。以上。
この思考過程が、すでに「証明」の基礎を成している。タレスの場合は、太陽の落とす影という自然現象(あるいは幾何学)を利用した素朴な証明だが、この考え方をさらに押し進めて、洗練させたのがピュタゴラスなのだよ。
では、われわれも、ピュタゴラスの思考に従い、ピュタゴラスの定理、別名、三平方(さんへいほう)の定理を証明してみよう……と、言いたいところだけど、いまでは、ピュタゴラスの定理を証明する方法が数百も知られている。中には、かのレオナルド・ダ・ビンチが考えた証明まである。
なのに、ああ、なのに、ピュタゴラスが考えた証明は、伝わっていないんだ。告白しよう。そもそも、ピュタゴラスが、この定理を証明したかどうかも、本当はわかっていない。だから彼の思考を追うことはできないのだ。
ただ、これだけは言える。ピュタゴラスは、この定理が普遍的に成り立つことを確信していた。そして、それが、どれほど重大な意味を持つのかも知っていたはずだ。
あまりにも重大な秘密なので、こうしてキーボードを打つ手が震えるが……みんなにも、お教えしよう。この定理の本当の意味を。
いいかい諸君。ピュタゴラスの定理は、すべての直角三角形について成り立つ。これは、直角そのものを定義することに等しい。すると直角は、垂線を定義することにも気づくだろう。垂線とは、平面に対して、垂直に交わる直線のことだ。要するに、地面に立っている、まっすぐな電信柱を想像すれば、それが垂線だ(えらく太っていて、かつ短すぎるけど)。
さあ、だんだん核心に近づいてきたぞ。そろそろ、驚く準備をしてくれた方がいい。いいかい、垂線が定義されると言うことは、水平と垂直が定義されると言うことだ。
水平と垂直……
ああ、なんということだ! それは、ぼくらが住む、この三次元空間のことではないか!
そう。これがピュタゴラスの定理に秘められたパワーだ。この定理は、ぼくらの住む、この空間の構造を示している。もし神がいたとして、神がこの空間を作ったのだとしたら、ぼくらは神の秘密をひとつ知ったことになるのだ。これが数学の魔力だ。一度虜になれば、もう逃れるすべはない……
だんだん、オカルトチックになってきたな。みんな、面食らった?(笑)。
ごめん、ごめん。これでも物書きなんでね。ついドラマチックに書きたくなるんだよ。でも、神を出したのは、ただドラマチックにしたいだけじゃない。ピュタゴラスは、数に神秘性を求めすぎたかもしれないのだ。だから彼は、矛盾を生む美しくない数字(概念)を嫌った。それは研究が遠からず行き詰まることを意味し、また彼自身の命を縮める原因にもなった。
ピュタゴラスが、神についてどういう思想を持っていたのか、本当のところはわからないのだけど、彼の開いたピュタゴラス教団は、学問所というより、宗教団体と呼ぶべきモノだった。教団の中で、どんな研究が行われているかは、当時から秘密のベールで覆われていた。だから教団のあったクロトンの人々は、ピュタゴラス教団を恐れるようになった。なにか邪悪な呪術が行われているという噂さえ立った。それが高じて、ついにピュタゴラスは、住民たちによって殺されてしまった。
皮肉なことに、ピュタゴラスが殺されることによって、教団の結束がゆるみ、何人かの弟子が教団を抜け出して、外の世界で、数学的知見を広めたので、ピュタゴラスの伝説が残ったのだ。
よしと……
どうやら、この辺がキリのいいところのようだ。エッセイは、なるべく一晩で書き終えることを自分に課してきたけど、このエッセイは二晩もかかった。しかも、数学について語り尽くしたとは、とても言えない。
そういえば思い出した。ぼくの尊敬するアイザック・アシモフのエッセイ集に「見果てぬ時空」という本がある。その本の序文に、こんな一節が載っていた。
サム・ヴォーンに捧げる。彼は
「たったいまアイザックが、一冊の本に許される長さの二倍もある自伝の原稿を持ち込んできました」
と聞かされたとき、雄々しくも答えた。
「二冊にしたまえ」と。
この法則に従って、数学に関するエッセイも、もう一回続けさせてもらおう。次回は、数学の世界に起こった、とんでもない革命について語ってみたい。その革命とは「ゼロ」の追加だ。
ゼロ……それは、不思議なパワーを秘めている。なにしろぼくらは、買ってきたリンゴをすべて食べてしまったとき、それを「ゼロ個のリンゴ」とは数えない。なのに数学者は、ゼロは数学になくてはならないと言うのだ。しかもゼロは、無限という悪魔の仲間なのだという……
もう次回のエッセイのタイトルも決まっている。ご存じの方もいるだろうが、かのアインシュタインの名言の冒頭を使わせていただくことにした。
「無限なものは二つある」
この言葉の続きは、次回のエッセイで明らかにしよう。
※追伸
ごめん、ごめん。本文の中で解説するのを、すっかり忘れていた。フェルマーの最終定理は、このエッセイで解説したピュタゴラスの定理を基礎としていると書いたね。その様子を、欄外で申し訳ないけどお見せしよう。
ピュタゴラスの定理は――
a2+b2=c2
だったね。
フェルマーの最終定理は――
xn+yn=zn (nは2よりも大きい自然数)
というものだ。いままで解説してきたように、このnが2であれば、それはピュタゴラスの定理そのものだから、整数解が無限に存在することがわかっている(なにしろ、すべての直角三角形について成り立つのだから)。
ところが、フェルマーは、その2を3に変えて計算してみた。すると、2のときは、無限にあった解が、ひとつも見つけられなかったんだよ。しかも、4でも5でも、6でもダメらしいのだ。そこでフェルマーは、nが2よりも大きいとき、この式に整数解はないと考えて研究し、ついに解がないことを証明したと主張した。ところが……おっと、ごめん。欄外が足りなくて、これ以上は書けない。あとは自分で調べてみてくれたまえ。 |
≫ Back
Copyright © TERU All Rights Reserved.
